🍀概要
情報処理技術者試験の中でも、最も権威あるとされている高度区分の問題は、午前1、午前2の出題が4択形式の試験です。①午前1は、全30問が出題され、合格ラインは18問以上の正解、②午前2は、全25問が出題され、合格ラインは15問以上の正解、とされています。しかし、もし一切知識がない状態でランダムにマークした場合、どれほどの確率で合格できるのでしょうか?
本記事では、この疑問に答えるため、モンテカルロシミュレーションを用いた確率シミュレーターを作成し、その詳細な結果とプログラムコードを公開します。
※本記事の執筆者は、中学校・高等学校教諭一種免許状(数学)を保有しており、数学的な観点から試験制度を分析しています。
🧾出題形式の基本
情報処理技術者試験の高度区分の午前問題は、以下の形式で出題されます。
- 出典: 情報処理推進機構 高度区分 情報処理技術者試験(🔗取り扱いガイドライン)
- 形式: 4択問題
- 問題数・合格基準:
- 午前1: 30問出題、18問以上の正解
- 午前2: 25問出題、15問以上の正解
📘モンテカルロシミュレーションとは?:実践的な確率計算アプローチ
情報処理推進機構 高度区分 情報処理技術者試験の午前1を題材に考えますと、30問中18問以上の正解を得る確率を厳密に数学的に計算するのは非常に複雑です。そこで登場するのが「モンテカルロシミュレーション」です。
これは、実際にランダムにマークシートを塗りつぶし、採点する試行を莫大な回数(例えば10万回)繰り返すことで、確率を近似的に求める手法です。
例えば、たった1回試行しただけでは、偶然の偏りが大きく、その結果は信頼できません。しかし、これを10万回、100万回と繰り返すことで、試行回数中に「合格基準に達した回数」を数え、「合格回数 ÷ 総試行回数 × 100%」と計算すれば、非常に高い精度で突破確率を推定できます。
まさに、この「サイコロを振るように何度も試行を重ねて、事象の発生確率を導き出す」のがモンテカルロシミュレーションの核心です。この考え方に基づいて、今回の確率計算を行います。
📗さらにリアルなシミュレーションを!:受験者の実力を加味した分析
実際の受験者が全問の答えを全く知らない、ということは稀でしょう。そこで、より現実に即したシミュレーションを行うために、以下の2つのシナリオも追加で分析しました。
- 「確実に得点できる問題」がある場合: 事前に一定数の問題が解けると仮定し、それ以外の問題をランダムにマークした場合の合格率を算出。
- 「選択肢を絞り込める学力」がある場合: 4択問題に対し、解答の精度を高める学力(例えば、誤りの選択肢を1つ除外して「3択」に絞り込める、あるいは2つ除外して「2択」にまで絞り込める)があるケースを想定し、それぞれの場合の合格率をシミュレーション。
これらの詳細なシミュレーション結果から、あなたの学習戦略を考える上での新たな視点が見つかるかもしれません。
💻プログラム
📝ソース ※中身知りたい人向け。コピペで使えます。
プログラムコード(Java)
IpaKoudoAmSimulator.java
--------------------------------------------------------------------------------------------
import java.util.Random;
/**
* IPA高度区分試験(午前1、午前2)の合格確率をモンテカルロシミュレーションで計算するシミュレーター。
* 各試験区分と解答方式(4択、3択、2択)に応じて合格率を算出します。
*/
public class IpaKoudoAmSimulator {
// 定数定義
private static final int DEFAULT_TRIALS = 100000; // 各シナリオでのデフォルト試行回数
/**
* IPA高度区分試験の種類を定義する列挙型。
* 各試験の総問題数と合格に必要な正解数を保持します。
*/
public enum ExamType {
ADVANCED_EXAM_AM1("高度区分 午前1問題", 30, 18),
ADVANCED_EXAM_AM2("高度区分 午前2問題", 25, 15);
private final String name;
private final int totalQuestions;
private final int passingScore;
ExamType(String name, int totalQuestions, int passingScore) {
this.name = name;
this.totalQuestions = totalQuestions;
this.passingScore = passingScore;
}
public String getName() {
return name;
}
public int getTotalQuestions() {
return totalQuestions;
}
public int getPassingScore() {
return passingScore;
}
}
/**
* 解答方式を定義する列挙型。
* 各方式の正答率を保持します。
*/
public enum AnswerMethod {
FOUR_CHOICES("4択問題", 4),
THREE_CHOICES("3択問題 (1つ除外)", 3),
TWO_CHOICES("2択問題 (2つ除外)", 2);
private final String name;
private final int totalChoices; // 選択肢の数
AnswerMethod(String name, int totalChoices) {
this.name = name;
this.totalChoices = totalChoices;
}
public String getName() {
return name;
}
public int getTotalChoices() {
return totalChoices;
}
}
/**
* シミュレーション結果を保持するレコード。
* (Java 16 以降で利用可能なレコード型を使用しています。古いJavaバージョンの場合は通常のクラスに変換してください)
*/
public record SimulationResult(int knownCorrectQuestions, double successRate) {}
private final Random random;
/**
* IpaKoudoAmSimulatorの新しいインスタンスを生成します。
*/
public IpaKoudoAmSimulator() {
this.random = new Random();
}
/**
* 指定されたシナリオでモンテカルロシミュレーションを実行し、合格確率を計算します。
*
* @param examType シミュレーション対象の試験タイプ
* @param answerMethod シミュレーション対象の解答方式
* @param knownCorrectQuestions 事前に知っている正解数
* @param trials 試行回数
* @return シミュレーション結果を表す {@code SimulationResult} オブジェクト
* @throws IllegalArgumentException 不正な引数が指定された場合
*/
public SimulationResult simulateScenario(ExamType examType, AnswerMethod answerMethod, int knownCorrectQuestions, int trials) {
if (knownCorrectQuestions < 0 || knownCorrectQuestions > examType.getTotalQuestions()) {
throw new IllegalArgumentException(
"事前に知っている正解数 (" + knownCorrectQuestions + ") は、0から総問題数 (" + examType.getTotalQuestions() + ") の範囲で指定してください。"
);
}
if (trials <= 0) {
throw new IllegalArgumentException("試行回数は1以上を指定してください。");
}
int totalQuestions = examType.getTotalQuestions();
int passingScore = examType.getPassingScore();
int successfulTrials = 0;
// 知っている問題以外の解答に必要な問題数と正解数
int remainingQuestions = totalQuestions - knownCorrectQuestions;
int requiredCorrectForPassing = passingScore - knownCorrectQuestions;
// 事前知識だけで合否が確定する場合の早期リターン
if (requiredCorrectForPassing <= 0) {
return new SimulationResult(knownCorrectQuestions, 100.00); // 確実に合格
}
if (requiredCorrectForPassing > remainingQuestions) {
return new SimulationResult(knownCorrectQuestions, 0.00); // 合格不可能
}
for (int i = 0; i < trials; i++) {
int guessedCorrect = 0;
for (int j = 0; j < remainingQuestions; j++) {
// 解答方式に応じた確率で正解をシミュレート
if (random.nextInt(answerMethod.getTotalChoices()) == 0) {
guessedCorrect++;
}
}
if (guessedCorrect >= requiredCorrectForPassing) {
successfulTrials++;
}
}
double successRate = (double) successfulTrials / trials * 100;
return new SimulationResult(knownCorrectQuestions, successRate);
}
/**
* シミュレーション結果を表示します。
*
* @param result 表示するシミュレーション結果
*/
public void displayResult(SimulationResult result) {
System.out.printf("・事前に%d問知っている場合: 合格率: %.2f%%\n", result.knownCorrectQuestions(), result.successRate());
}
/**
* メインメソッド。各種IPA高度区分試験のシミュレーションを実行します。
*/
public static void main(String[] args) {
IpaKoudoAmSimulator simulator = new IpaKoudoAmSimulator();
System.out.println("★IPA高度区分マーク試験突破確率計算:ランダム選択方式(モンテカルロシミュレーション)★");
System.out.println(); // 空行を追加して見やすく
// 各試験タイプと解答方式の組み合わせでシミュレーションを実行
for (ExamType examType : ExamType.values()) {
System.out.println("---");
System.out.println("■" + examType.getName() + " (総問題数: " + examType.getTotalQuestions() + "問, 合格に必要な正解数: " + examType.getPassingScore() + "問)");
System.out.println("---");
for (AnswerMethod answerMethod : AnswerMethod.values()) {
System.out.println(" ◇ " + answerMethod.getName() + " 試行結果");
// シミュレーション対象の knownCorrectQuestions の範囲を合格点までにする
for (int i = 0; i <= examType.getPassingScore(); i++) {
try {
SimulationResult result = simulator.simulateScenario(examType, answerMethod, i, DEFAULT_TRIALS);
simulator.displayResult(result);
} catch (IllegalArgumentException e) {
System.err.println("エラー: " + e.getMessage());
}
}
System.out.println(); // 各解答方式の後に空行
}
}
System.out.println("---");
}
}▶️WEB実行環境
glot.ioというWEB上でプログラムを誰でも実行できるページあったので、作ってみました。以下から実行(Run)できます。
https://glot.io/snippets/h9hip43cek
🧭実行結果
各10万回試行した、実行結果ログ ※長いので、折りたたみます。
★IPA高度区分マーク試験突破確率計算:ランダム選択方式(モンテカルロシミュレーション)★
---
■高度区分 午前1問題 (総問題数: 30問, 合格に必要な正解数: 18問)
---
◇ 4択問題 試行結果
・事前に0問知っている場合: 合格率: 0.01%
・事前に1問知っている場合: 合格率: 0.02%
・事前に2問知っている場合: 合格率: 0.03%
・事前に3問知っている場合: 合格率: 0.06%
・事前に4問知っている場合: 合格率: 0.14%
・事前に5問知っている場合: 合格率: 0.31%
・事前に6問知っている場合: 合格率: 0.73%
・事前に7問知っている場合: 合格率: 1.50%
・事前に8問知っている場合: 合格率: 2.97%
・事前に9問知っている場合: 合格率: 5.60%
・事前に10問知っている場合: 合格率: 10.12%
・事前に11問知っている場合: 合格率: 17.46%
・事前に12問知っている場合: 合格率: 28.14%
・事前に13問知っている場合: 合格率: 42.78%
・事前に14問知っている場合: 合格率: 59.76%
・事前に15問知っている場合: 合格率: 76.51%
・事前に16問知っている場合: 合格率: 90.07%
・事前に17問知っている場合: 合格率: 97.59%
・事前に18問知っている場合: 合格率: 100.00%
◇ 3択問題 (1つ除外) 試行結果
・事前に0問知っている場合: 合格率: 0.22%
・事前に1問知っている場合: 合格率: 0.44%
・事前に2問知っている場合: 合格率: 0.78%
・事前に3問知っている場合: 合格率: 1.44%
・事前に4問知っている場合: 合格率: 2.46%
・事前に5問知っている場合: 合格率: 4.14%
・事前に6問知っている場合: 合格率: 6.71%
・事前に7問知っている場合: 合格率: 10.64%
・事前に8問知っている場合: 合格率: 16.34%
・事前に9問知っている場合: 合格率: 24.15%
・事前に10問知っている場合: 合格率: 33.95%
・事前に11問知っている場合: 合格率: 46.01%
・事前に12問知っている場合: 合格率: 58.85%
・事前に13問知っている場合: 合格率: 71.77%
・事前に14問知っている場合: 合格率: 83.39%
・事前に15問知っている場合: 合格率: 92.19%
・事前に16問知っている場合: 合格率: 97.20%
・事前に17問知っている場合: 合格率: 99.46%
・事前に18問知っている場合: 合格率: 100.00%
◇ 2択問題 (2つ除外) 試行結果
・事前に0問知っている場合: 合格率: 18.10%
・事前に1問知っている場合: 合格率: 22.81%
・事前に2問知っている場合: 合格率: 28.59%
・事前に3問知っている場合: 合格率: 35.08%
・事前に4問知っている場合: 合格率: 42.12%
・事前に5問知っている場合: 合格率: 50.12%
・事前に6問知っている場合: 合格率: 57.91%
・事前に7問知っている場合: 合格率: 66.16%
・事前に8問知っている場合: 合格率: 73.87%
・事前に9問知っている場合: 合格率: 80.72%
・事前に10問知っている場合: 合格率: 86.74%
・事前に11問知っている場合: 合格率: 91.53%
・事前に12問知っている場合: 合格率: 95.26%
・事前に13問知っている場合: 合格率: 97.53%
・事前に14問知っている場合: 合格率: 98.94%
・事前に15問知っている場合: 合格率: 99.63%
・事前に16問知っている場合: 合格率: 99.92%
・事前に17問知っている場合: 合格率: 99.98%
・事前に18問知っている場合: 合格率: 100.00%
---
■高度区分 午前2問題 (総問題数: 25問, 合格に必要な正解数: 15問)
---
◇ 4択問題 試行結果
・事前に0問知っている場合: 合格率: 0.02%
・事前に1問知っている場合: 合格率: 0.06%
・事前に2問知っている場合: 合格率: 0.11%
・事前に3問知っている場合: 合格率: 0.27%
・事前に4問知っている場合: 合格率: 0.65%
・事前に5問知っている場合: 合格率: 1.30%
・事前に6問知っている場合: 合格率: 2.85%
・事前に7問知っている場合: 合格率: 5.66%
・事前に8問知っている場合: 合格率: 10.61%
・事前に9問知っている場合: 合格率: 19.16%
・事前に10問知っている場合: 合格率: 31.51%
・事前に11問知っている場合: 合格率: 47.72%
・事前に12問知っている場合: 合格率: 66.66%
・事前に13問知っている場合: 合格率: 84.13%
・事前に14問知っている場合: 合格率: 95.79%
・事前に15問知っている場合: 合格率: 100.00%
◇ 3択問題 (1つ除外) 試行結果
・事前に0問知っている場合: 合格率: 0.57%
・事前に1問知っている場合: 合格率: 1.02%
・事前に2問知っている場合: 合格率: 1.91%
・事前に3問知っている場合: 合格率: 3.30%
・事前に4問知っている場合: 合格率: 5.62%
・事前に5問知っている場合: 合格率: 9.17%
・事前に6問知っている場合: 合格率: 14.63%
・事前に7問知っている場合: 合格率: 22.19%
・事前に8問知っている場合: 合格率: 32.30%
・事前に9問知っている場合: 合格率: 45.26%
・事前に10問知っている場合: 合格率: 59.63%
・事前に11問知っている場合: 合格率: 74.09%
・事前に12問知っている場合: 合格率: 86.27%
・事前に13問知っている場合: 合格率: 94.65%
・事前に14問知っている場合: 合格率: 98.83%
・事前に15問知っている場合: 合格率: 100.00%
◇ 2択問題 (2つ除外) 試行結果
・事前に0問知っている場合: 合格率: 21.18%
・事前に1問知っている場合: 合格率: 27.01%
・事前に2問知っている場合: 合格率: 33.89%
・事前に3問知っている場合: 合格率: 41.47%
・事前に4問知っている場合: 合格率: 50.23%
・事前に5問知っている場合: 合格率: 58.88%
・事前に6問知っている場合: 合格率: 67.77%
・事前に7問知っている場合: 合格率: 76.08%
・事前に8問知っている場合: 合格率: 83.29%
・事前に9問知っている場合: 合格率: 89.51%
・事前に10問知っている場合: 合格率: 93.87%
・事前に11問知っている場合: 合格率: 97.13%
・事前に12問知っている場合: 合格率: 98.85%
・事前に13問知っている場合: 合格率: 99.68%
・事前に14問知っている場合: 合格率: 99.94%
・事前に15問知っている場合: 合格率: 100.00%
---
🎲午前1 シミュレーション結果:30問中の戦略
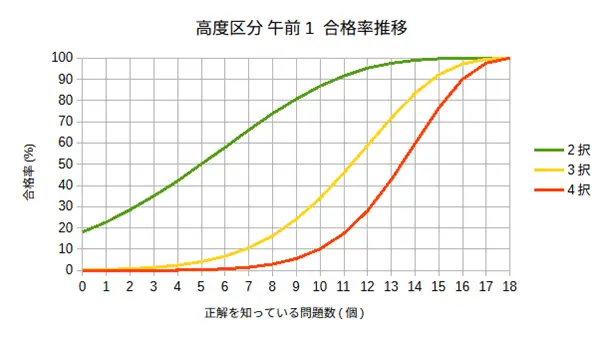
🌧️午前1 シミュレーション結果:30問中の戦略
「4択の絞り込みができないレベル」の場合、事前に10問の答えを知っていても合格率はわずか10%前後という厳しい結果に。これは、全30問中、残りの20問から合格ライン(18問正解)に達する8問を、知識がない状態で正解することの極めて高いハードルを示しています。また、完全にランダムにマークした場合は、合格率が0%となり、運任せでは合格が不可能であることを明確に示しています。
合格率を90%以上に引き上げるには、このレベルでは事前に16問以上を確実に正解できる実力、つまり総問題数の半分以上を完璧に理解している必要があることがわかります。
☀️希望の光:2択まで絞り込める場合
一方、「2択の絞り込みまでできるレベル」では、明るい兆しが見えてきます。この場合、事前に11問の答えを知っていれば、合格率を90%以上に高められるという結果が出ました。
この分析からわかるのは、たとえ全問を完璧に解答できなくても、不正解の選択肢を確実に絞り込む努力が、合格への大きな鍵となるということです。知識を深めて選択肢を減らす力を養うことが、合格への道を大きく開くでしょう。
⛳午前2 シミュレーション結果:25問中の集中力
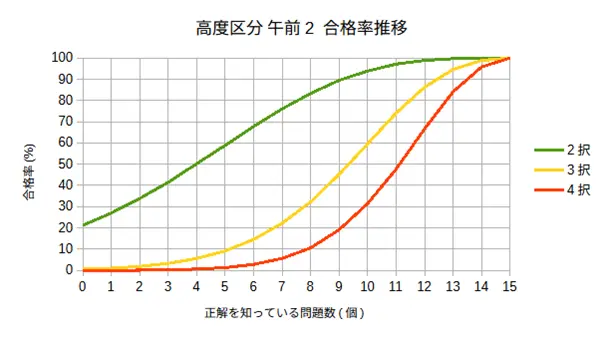
午前1と同様の傾向が見られるものの、午前2は問題数が少ない分、運の要素が合格に与える影響がより大きくなる傾向が見られました。
🌧️厳しい現実:完全ランダムと4択絞り込み不可の場合
「4択の絞り込みができないレベル」では、事前に8問の答えを知っていても合格率は10%程度と、やはり厳しい結果です。これは、単に多くの問題をこなすだけでなく、選択肢を減らす能力がいかに重要であるかを物語っています。当然ながら、完全にランダムにマークした場合は合格率0%で、午前1同様、運任せの合格は極めて困難です。
合格率を90%以上に引き上げるには、このレベルでは事前に14問以上を確実に正解できる実力が必要です。問題数が25問と少ないため、わずか1問の差が合否を分ける可能性があり、運悪く連続して間違えると不合格になるリスクが高まります。
☀️希望の光:2択まで絞り込める場合
しかし、「2択の絞り込みまでできるレベル」では、希望が見えてきます。このレベルであれば、事前に9問の答えを知っていれば、合格率を90%以上に高めることができるという結果が出ました。
このシミュレーション結果から、午前2においても、たとえ完璧な知識がなくても、不正解の選択肢を確実に絞り込む努力が、合格への重要な鍵となることがわかります。諦めずに知識を深め、選択肢を減らす力を養うことが、合格への道を大きく開くでしょう。
今回のシミュレーションが、あなたの学習戦略を練る上での一助となれば幸いです。
